About Bach’s Tuning Method – 2
Pythagorean 5th degree … About 701.96 cents
The fifth degree of the meantone … 696.5 cents
The fifth degree of the equal temperament … 700 cents
700✕12 = 8,400 … the cents of the fifth degree of the equal temperament✕12
701.96✕12 = 8,423.52 … the number of cents in the Pythagorean fifth degree✕12
*The error is 23.52 cents (Pythagorean comma)
701.96✕4 = 2,807.84 … Pythagorean fifth degree✕4
Approximately 696.5 cents✕4 = 2,786 … 5 degrees O 4 of the meantone
*The error is 21.84 cents (syntonic comma)
23.52 – 21.84 = 1.68 cents (scisma) * difference between Pythagorean comma and syntonic comma
————————————————–
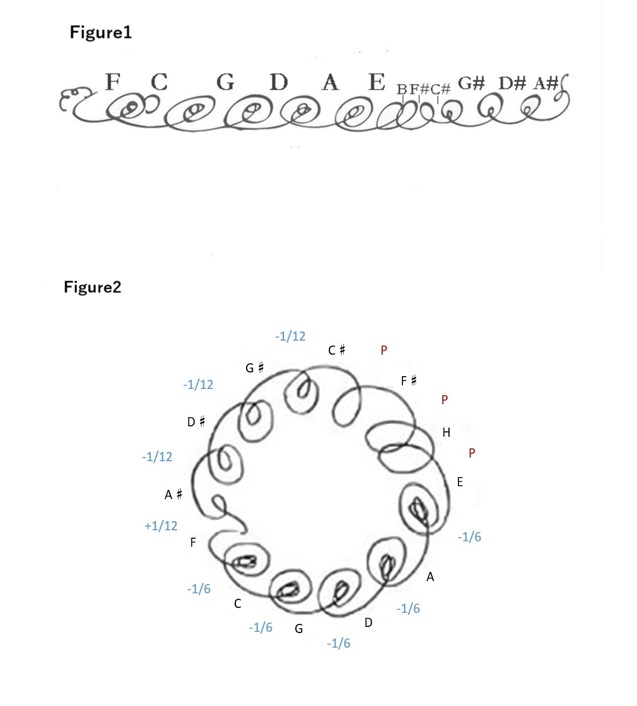
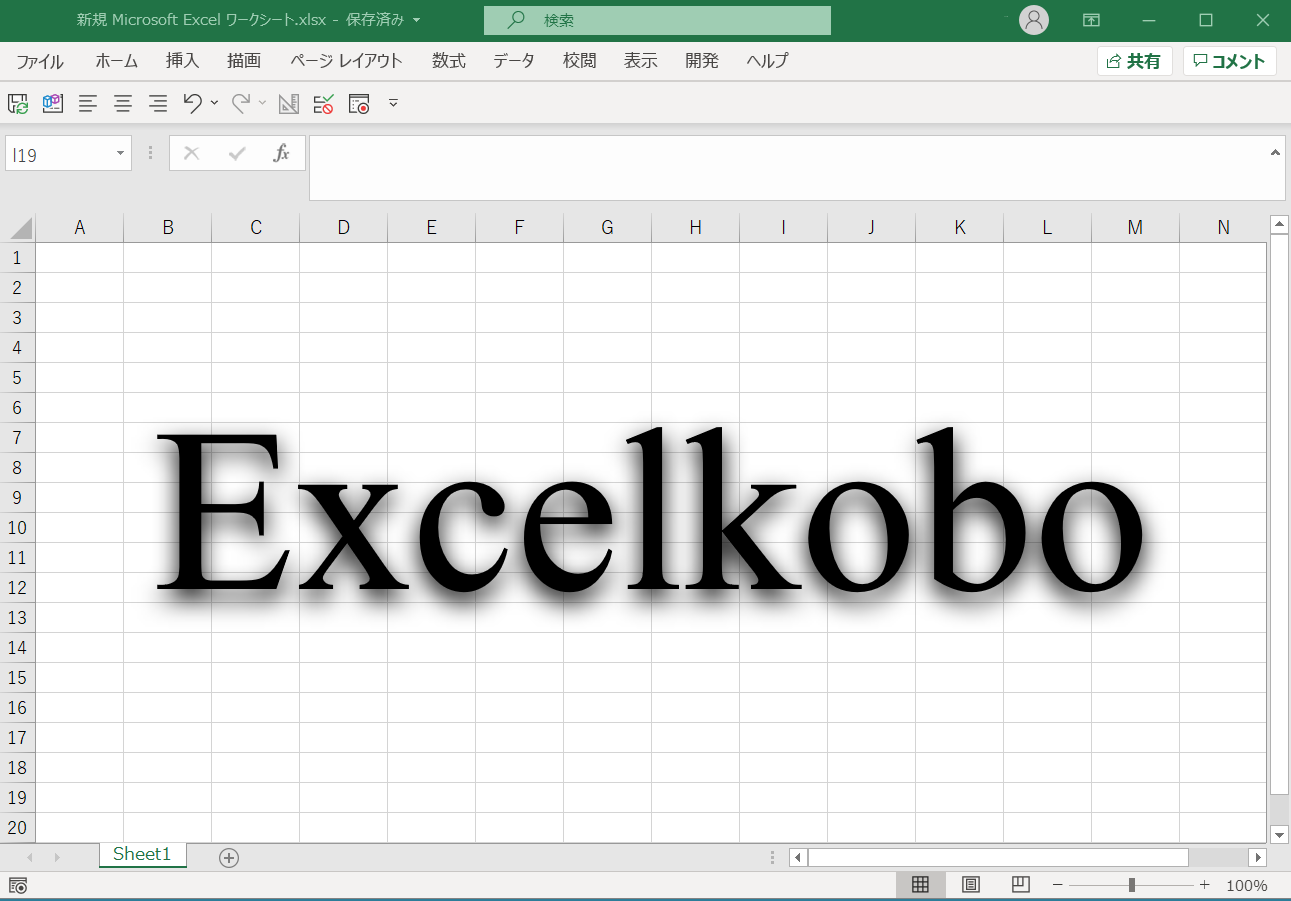
I would like to present another hypothesis. It is Bradley Lehmann’s. He turned Bach’s figure upside down (Figure 1) and created a circle starting at F. (Figure 2) The numerical values of his hypothesis are as follows.
Example of Bach’s Tuning Method Answer (by Bradley Lehman)
*Bach’s figures
(1) Triple circle … Pythagorean fifth degrees – comma 1/6 (five)
(2) Single circle … Pythagorean fifth degrees (three)
(3) Double circle … Pythagorean fifth degree – comma 1/12 (three)
(4) Between A# and F … fifth degree of Pythagoras + comma 1/12 (one)
*Calculation
(1) (701.96 – 23.52✕1/6)O5 = (701.96 – 3.92)O5 = 698.04✕5 = 3,490.2
(2) 701.96✕3 = 2,105.88
(3) 701.96✕3 = (701.96 – 23.52✕1/12)✕3 = (701.96 – 1.96)✕3 = 2,100
(4) 701.96 + 1.96 = 703.92
(1) + (2) + (3) + (4) = 3,490.2 + 2,807.84 + 2,100 + 703.92 = 8,400
It is important to note the figure “Pythagorean fifth degree – comma 1/12”, which is, in essence, the fifth degree of the “equal temperament”. If Bach was able to create this interval, why did he not come up with the idea of the “equal temperament” for all the fifth? That is my question. #baroque #bach #temperament #片山俊幸