About so-called “Well-Tempered”

Pythagorean 5th degree … about 701.96 cents

The fifth degree of the meantone … about 696.5 cents

The fifth degree of the equal temperament … 700 cents

700✕12 = 8,400… the number of cents per fifth degree of the equal temperament✕12

701.96✕12 = 8,423.52 … the number of cents in the fifth degree of Pythagoras✕12

*The error is 23.52 cents (Pythagorean comma)

701.96✕4 = 2,807.84 … Pythagorean fifth degree✕4

Approximately 696.5 cents✕4 = 2,786 … 5 degrees of the meantone✕4

*The error is 21.84 cents (syntonic comma)

23.52 – 21.84 = 1.68 cents (scisma) *Difference between the Pythagorean comma and the syntonic comma

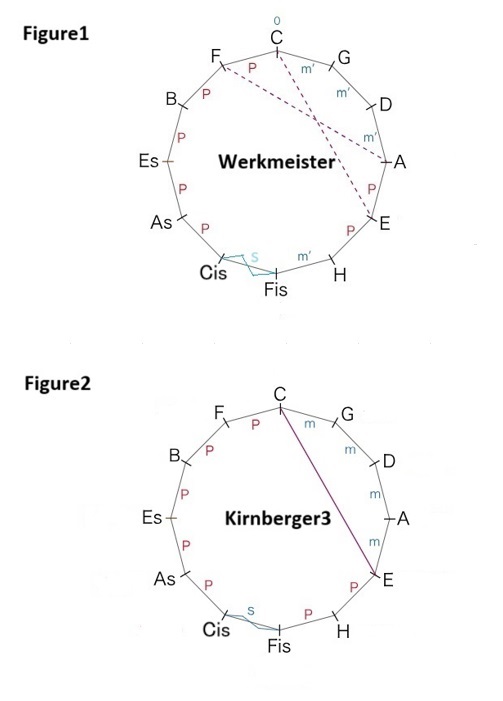
There are two tuning methods called “Werckmeister Ⅲ” and “Kirnberger Ⅲ” that are thought to have been used as so-called “Well-Tempered” in Bach’s time.

The “Werckmeister Ⅲ” uses meantone fifth degrees in four places: three fifths (C-G, G-D, D-A) and one (H-F♯). Of the remaining five degrees, (A-E,E-H) and fifths backwards from C to A♭(C-F,F-B♭,B♭-E♭,E♭-A♭), for a total of seven Pythagorean fifths are used. Then the last remaining (F♯-C♯) is used to adjust the error. (Figure 1)

*Calculation

696.5✕4 = 2,786

701.96✕7 = 4,913.72

701.96 – 1.68 = 700.28 … *1.68 cents (scisma)

2,786+4,913.72+700.28 = 8,400

The “Kirnberger Ⅲ” uses four fifth degrees of the meantone (C-G,G-D,D-A,A-E). And two Pythagorean fifths (E-H,H-F♯), and five Pythagorean fifths backwards from C to A♭(C-F,F-B♭,B♭-E♭,E♭-A♭), for a total of seven Pythagorean fifths. Then, the last remaining (F♯-C♯) is used to adjust the error. (Figure 2)

*Calculation

696.5✕4 = 2,786

701.96✕7 = 4,913.72

701.96 – 1.68 = 700.28 … * 1.68 cents (scisma)

2,786+4,913.72+700.28 = 8,400

Although numerically similar, there is one “genuine major third degree” in the “Kirnberger” but not in the “Werckmeister Ⅲ”. #baroque #Kirnberger #werckmeister #temperament #片山俊幸