About Vallotti temperament

Pythagorean 5th degree … about 701.96 cents

The fifth degree of the meantone … about 696.5 cents

The fifth degree of the equal temperament … 700 cents

700✕12 = 8,400… the number of cents per fifth degree of the equal temperament✕12

701.96✕12 = 8,423.52 … the number of cents in the fifth degree of Pythagoras✕12

*The error is 23.52 cents (Pythagorean comma)

701.96✕4 = 2,807.84 … Pythagorean fifth degree✕4

Approximately 696.5 cents✕4 = 2,786 … 5 degrees of the meantone✕4

*The error is 21.84 cents (syntonic comma)

23.52 – 21.84 = 1.68 cents (scisma) *Difference between the Pythagorean comma and the syntonic comma

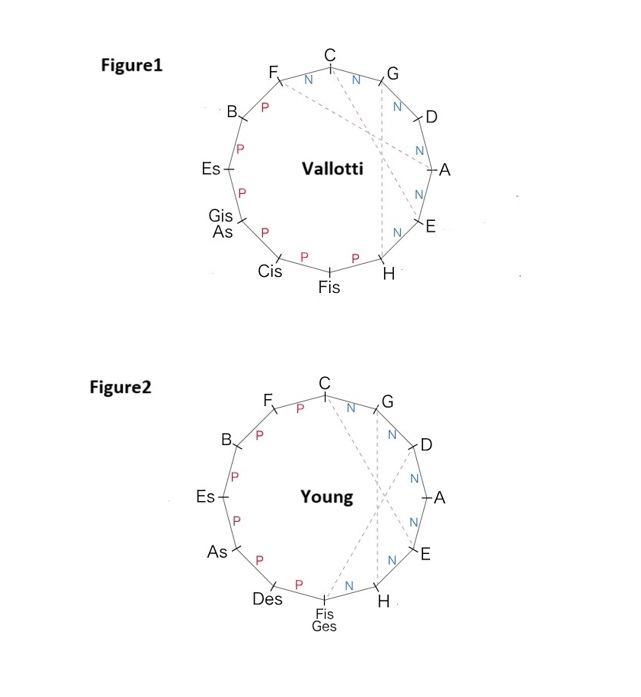
Vallotti’s tuning consists of six Pythagorean fifths narrowed by 1/6th syntonic comma, five Pythagorean fifths, and one Pythagorean fifths narrowed by scisma (difference between the Pythagorean and syntonic commas, about 1.68 cents).

*Calculation

(701.96-21.84/6)✕6 = (701.96-3.64)✕6 = 4189.92 cents

701.96✕5 = 3,509.8 … Pythagorean 5 degrees✕5 cents

701.96 – 1.68 = 700.28 … the number of cents in Pythagorean fifth degree – scisma

4189.92+3,509.8+700.28 = 8,400

This “five-degree circle” begins at F. In addition, Vallotti does not mention in which position the fifth degree, which is narrowed only by the scisma, should be placed. Therefore, in general, Vallotti’s tuning scheme is often interpreted as follows.(Figure1)

(701.96 – 23.52/6)✕6 = 4,188.24…(Pythagorean fifth degree – Pythagorean comma✕1/6)✕6 cents

701.96✕6 = 4,211.76… Pythagorean fifth degree✕6 cents

4,188.24 + 4,211.76 = 8,400

Note that the “Young’s tuning”(Figure2) is a tuning that starts this circle at C. These two tunings have basically the same structure. Both were a type of “Well-Tempered” that could be played without having to retune all the tonalities.

—————————————–

Physics is a discipline that falls somewhere between mathematics and music. The first person to attempt to explain music with mathematics (or mathematics with music) was Pythagoras, born in 582 BC in Greek. The Pythagorean temperament were subsequently adopted throughout Europe, and his theory was faithfully followed until the Middle Ages. In the Renaissance period, intervals not mentioned by Pythagoras (major third, minor third, seventh, etc.) came into use. This is when the idea of tuning was born, but it soon became clear that “tonal music” could not be explained solely by Pythagorean tuning. From that time on, physicists and musicians in Europe began to struggle against temperament method. After about 200 years of trial and error, the “Equal Temperament” method was discovered around 1750. However, in faraway China, the “Equal Temperament” had already been discovered and put into practical use around 1600. The discoverer was a scholar named Zhu Zai-yu. The reason for the delay in discovery in Europe is thought to be the fact that European music had “harmony”. In other words, the existence of the major third degree caused them to hesitate about the idea of the “Equal Temperament”. They had to experiment with all kinds of tuning method before they arrived at the “Equal Temperament”. Conversely, it is inevitable that Chinese music, which has no harmony, was able to reach this idea with ease. #baroque #vallotti #temperament #片山俊幸